Date
FacebookTwitterLinkedInWhatsAppCopy Site URL
Phase diagram of the lattice Abelian-Higgs model as seen through the lens of entanglement entropy. At small couplings, the system occupies two qualitatively different regions, a confined and a Higgs region, separated by a line of first order quantum phase transition (FOQPT). The line of FOQPT ends at a second order quantum phase transition (SOQPT).

A team of researchers from Jagiellonian University of Cracow, ICFO, the Institute of Cosmos Sciences of the University of Barcelona and CSIC uncovers hidden gems lurking behind the Abelian-Higgs model in one spatial dimension and time in a recent study published in Physical Review Letters.

While universal quantum computers with arbitrarily low logical error rates remain elusive, the future belongs to special purpose quantum computers, i.e. quantum simulators. Although there are no rigorous proofs, the physics community strongly believes that quantum simulators have already led to quantum advantage, especially, in studies of quantum dynamics and quantum disordered systems. So far, most of the applications of quantum simulators have concerned models of condensed matter physics. However, this paradigm is beginning to change, and more and more impressive applications are coming up. In physics, the current focus is on quantum simulation of fundamental models of high energy physics: Lattice Gauge Theories and Quantum Field Theories.

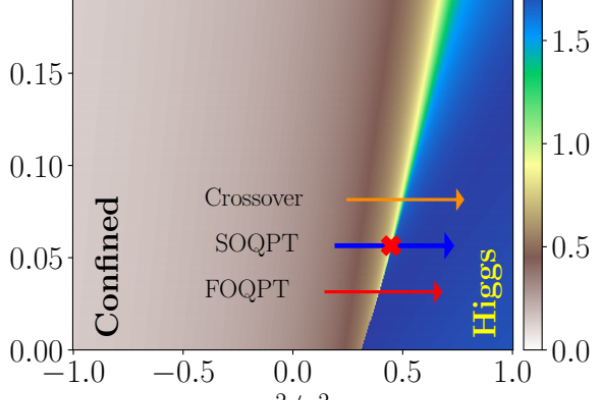
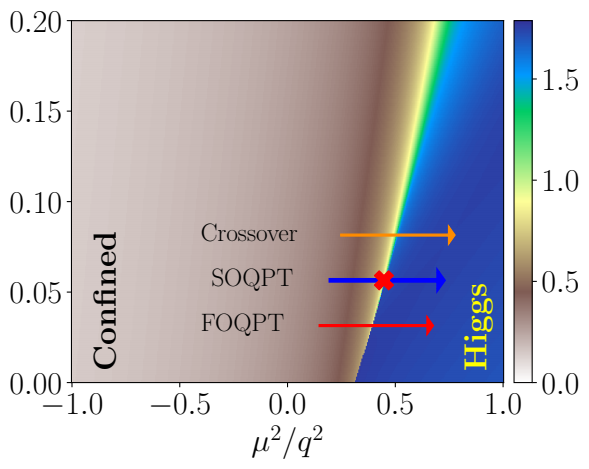
The Higgs mechanism is an essential ingredient of the Standard Model of particle physics that explains the ‘mass generation’ of gauge bosons. While its seemingly simple one-dimensional lattice version may serve as an interesting novel quantum simulator, until now, it remained unexplored. This mechanism is absent in one spatial dimension when taking a continuum approach, due to the absence of propagating gauge fields and to other non-perturbative effects. The recent calculations of the lattice version of the model however unveil some hidden gems, which are the remnant of the 1D Higgs mechanism. They consist in the appearance of two distinct regions in the lattice version, namely the confined and the Higgs regions, separated by a line of first order phase transitions that ends in a second order critical point. Above this critical point, the regions are smoothly connected by a crossover. The presence of a second order critical point allows one to construct an unorthodox continuum limit of the theory that is described by a conformal field theory (CFT).

Our result thus shows that the 1D Abelian Higgs model, which has priorly been overlooked, could provide an interesting system where a plethora of exotic features appears. The system thus requires further analysis, whose characterization on the next generation of quantum simulators would provide important insights on the phase diagram and out-of-equilibrium properties of the model.

This work is strongly motivated by the current prospects of quantum simulations of quantum gauge theories, and opens a path towards observing the Higgs mechanism in experiments with cold atomic setups.

 

Phase diagram of the lattice Abelian-Higgs model as seen through the lens of entanglement entropy. At small couplings, the system occupies two qualitatively different regions, a confined and a Higgs region, separated by a line of first order quantum phase transition (FOQPT). The line of FOQPT ends at a second order quantum phase transition (SOQPT).
 Phase diagram of the lattice Abelian-Higgs model as seen through the lens of entanglement entropy. At small couplings, the system occupies two qualitatively different regions, a confined and a Higgs region, separated by a line of first order quantum phase transition (FOQPT). The line of FOQPT ends at a second order quantum phase transition (SOQPT).

 

References

DOI: 10.1103/PhysRevLett.128.090601